Опубликовано 14.06.2001
© Паша Малинников, 18 Ноября
2000 г.
Это еще один из вопросов, который вам рано или поздно придется решать. В 3D графике без этого не обойтись, вне зависимости от того, используете ли вы какой-нибудь 3D API, как, например, OpenGL, или пишете от начала до конца движок сами.
Координаты точки пересечения отрезка с плоскостью в пространстве могут быть найдены различными способами, мы рассмотрим сейчас только один, на мой взгляд, самый удобный, способ, основанный на свойствах скалярного произведения векторов.
Давайте припомним, что же такое скалярное произведение векторов, и какими свойствами оно обладает. Я точно не знаю, но наверняка в средней школе нам давали определение типа; “скалярным произведением двух векторов называется число, равное произведению их длин, умноженному на косинус угла между ними”.
И видимо нас, как прилежных школьников, немедленно должна была потрясти мысль, что иными словами, “скалярное произведение двух векторов равно длине одного из них, помноженной на проекцию другого вектора на направление первого”, а ведь это значит, что при скалярном умножении вектора А на единичный вектор мы получаем проекцию этого вектора А на направление единичного вектора.
Должен честно признаться, что меня лично эта мысль нисколько не
потрясла (потому что не посетила), наверняка я был занят более важными делами
J.

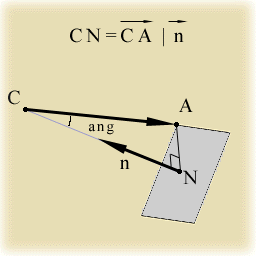
Однако, из рисунка видно, что с помощью скалярного произведения
векторов СА и n можно найти длину вектора CN, поскольку она
равна произведению длин:
Если это кажется не совсем очевидным, то под умайте о том, что отрезок CN на самом деле проекция вектора СА на направление нормали, а следовательно, CN = СА*cos(ang). А коль скоро длина вектора n равна 1, то никакого влияния на результат произведения она не оказывает.
Еще раз повторю, что расстояние CN, которое, по сути, является кратчайшим расстоянием от точки С до исследуемой плоскости, может быть найдено с помощью одной лишь операции скалярного произведения векторов, которая использует лишь операции сложения и умножения, так что ни угол ang, ни косинус этого угла находить не придется.
Единичный вектор n есть нормаль к плоскости, и может быть найдена способом, описанным в статейках “К вопросу о перпендикулярности полигона к вектору” и “Некоторые примеры использования векторов”.
Условимся обозначать скалярное произведение знаком | (вертикальная черта), оно рассчитывается следующим образом:
A | B = A.x* B.x + A.y* B.y + A.z* B.z
Другие виды векторных операций и сам класс CVector можно найти в Приложении № 1. Ну что же, будем считать, что со скалярным произведением мы разобрались. Давайте посмотрим, чем нам может помочь знание кратчайшего расстояния до плоскости в определении координат точки пересечения отрезка, заданного координатами 2-х точек в пространстве, и плоскости, заданной координатами 3-х точек (то, что 3-х достаточно, я помню после школы хорошо J).
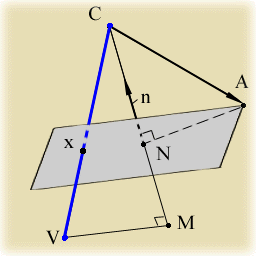
Предположим, нужно найти координаты точки х, образованной пересечением отрезка CV и плоскости, фрагмент которой показан на рисунке таким сереньким цветом.
Очевидно, точка х будет лежать на отрезке CV и делить его в таком же отношении, как относятся друг к другу отрезки CN и CM. А эти отрезки есть не что иное, как проекции векторов CA и CV на направление нормали и могут быть найдены при помощи способа, описанного выше.
Таким, образом, для нахождения координат точки х последовательность действий будет следующей:
x.x = CV.x * K
x.y = CV.y * K
x.z = CV.z *
K
Кроме того, необходимо учитывать, что отрицательное значение коэффициента К свидетельствует о том, что начальная точка (в нашем случае С) находится позади плоскости, другими словами, в в одном полупространстве с точкой V.
Если же коэффициент К больше 1, то можно говорить о том, что отрезок не достиг плоскости и пересечения не произошло.
*Реальный пример класса, позволяющий использовать все операции
над векторами, приведен в Приложении
№ 1
* В моих статьях описываются алгоритмы, не все из которых являются классическими или полностью совершенными. Поэтому приветствуются любые замечания, комментарии и критика.